(급하신 분들은 여기 단락은 안 읽으셔도 됩니다!)
안녕하세요. 한동안 또 글을 못쓰다가 오랜만에 쓰게 됐습니다. 원래대로라면 Neural Collaborative Filtering 코드를 올리려했으나 아직 완성되지 않아서 우선은 다른 논문을 먼저 올리게 되었습니다. 추천 시스템 입문하시는 분이시라면 이 논문을 먼저 보시는 것도 좋을 것이라 생각이 듭니다.
서론
이번 시간에는 Item-Based Collaborative Filtering 모델입니다. 추천시스템에서 흔히 나오는 Collaborative Filtering 중에서 top-K개를 활용할 때 User-Based로 하느냐, Item-Based로 하느냐로 갈리기도 하는데 여기서는 Item-Based입니다. 간단하게 Collaborative Filtering은 user가 item에 준 점수, 클릭 수 등 user와 item의 관계정보를 기반으로 추천하는 방식입니다. item을 기준으로 추천하면 item-Based(또는 item to item)이라 하고 user를 기준으로 하면 user-Based(또는 user to user)라고 합니다. 이에 대한 기초적인 부분이 필요하시다면 아래 제가 쓴 글을 보시는 것도 좋을 것 같습니다.
추천시스템 - 기초
안녕하세요! 오랜만에 글을 올립니다!! 이것저것 하다보니 글을 자꾸 못쓰다가 이제야 쓰게 되었습니다.. * 글에서 잘못된 부분이 있어 수정해서 다시 올립니다. 이번에는 추천시스템에 대해 살
hwa-a-nui.tistory.com
기존 방법의 한계점
저자는 user-Based collaborative filtering의 한계점을 다음과 같이 정의하고 있습니다.
○ Sparsity : 유저 대부분은 전체 item의 1% 정도만 구매하기 때문에 나머지 item에 대해선 NaN값으로 됩니다. 나머지는 NaN 값이기 때문에 사실상 특정 user의 Nearest Neighbor한 user를 구하기 어렵다고 말합니다.
○ Scalability : Nearest neighbor algorithm은 user와 item 숫자에 비례하여 계산 시간이 증가합니다. (이 부분은 사실 Nearest neighbor algorithm을 쓰는 모든 모델의 문제이기도 합니다)
이외의 여러 이유들로 저자는 item Based 방식을 제안합니다.
Item-Based Collaborative Filtering
알고리즘은 크게 다음과 같은 단계로 구성됩니다.
○ item 간 유사도 측정
○ 유사도를 바탕으로 Weighted sum이나 regression으로 예측값 구하기
먼저 유사도 측정부터 보겠습니다.
1. 유사도 측정
유사도 측정 방법은 크게 3가지로 나뉩니다. (자연어를 공부해보신 분들이면 익숙한 방법들이 보일거에요)
○ Cosine Similarity
- Cosine 유사도를 이용하여 item 간 유사도를 측정하는 방법으로 -1 ~ 1값을 가집니다.
- 식은 다음과 같습니다.
- $sim(i,j) = \frac{\sum_{u \in U} R_{u,i} * R_{u,j} }{\sqrt{\sum_{u \in U} (R_{u,i})^{2}} * \sqrt{\sum_{u \in U} (R_{u,j})^{2}}}$
- $U$ : item i와 j를 모두 평가한 user(1개만 평가한 user는 제외됩니다)
- $R_{u,i}$ : user u의 item i에 대한 점수
- $R_{u,j}$ : user u의 item j에 대한 점수
○ Correlation Similarity
- pearson 상관계수를 이용하여 item간 유사도를 측정하는 방법으로 -1 ~ 1값을 가집니다.
- 식은 다음과 같습니다.
- $sim(i,j) = \frac{ \sum_{u \in U} (R_{u,i} - \bar{R_{i}}) (R_{u,j} - \bar{ R_{j} } ) }{ \sqrt{ \sum_{u \in U} (R_{u,i} - \bar{R_{i}})^{2} } \sqrt{\sum_{u \in U} (R_{u,j} - \bar{R_{j}}})^{2} }$
- cosine similarity와 같은 변수는 똑같은 의미의 변수입니다.
- $\bar{R_{i}}$ : item i를 평가한 user들의 item i의 평균 점수입니다. (평가하지 않은 사람은 제외되며 j는 item j를 의미합니다.)
○ Adjusted Cosine Similarity
- Cosine Similarity에서 서로 다른 두 유저가 4점을 주었을 때 그 4점이 어떤 유저에게는 많이 준 것일 수도 있고 어떤 유저는 평균적으로 4점을 주는 것일 수도 있으나 이를 반영하지 못합니다.
- 이를 반영하기 위해 조정된 Cosine 유사도를 추가했습니다.
- 식은 다음과 같습니다.
- $ sim(i,j) = \frac{ \sum_{u \in U} ( R_{u,i} - \bar{R_{u}} )( R_{u,j} - \bar{R_{u}} ) }{ \sqrt{ \sum_{u \in U} (R_{u,i} - \bar{R_{u}})^{2} } \sqrt{ sum_{u \in U} (R_{u,j} - \bar{ R_{u} } )^{2} }} $
- 역시 cosine similarity와 같은 변수는 똑같은 의미의 변수입니다.
- $\bar{R_{u}}$ : user u의 평균 점수입니다. (user u가 평가하지 않은 0점 item은 제외됩니다.)
이 논문의 경우 일부 설명이 부족한 점도 있지만 알고리즘 원리 자체에 대한 설명은 세세하게 되어있습니다. 가령, 유사도를 계산할 때 예시로 다음과 같은 그림이 있습니다.
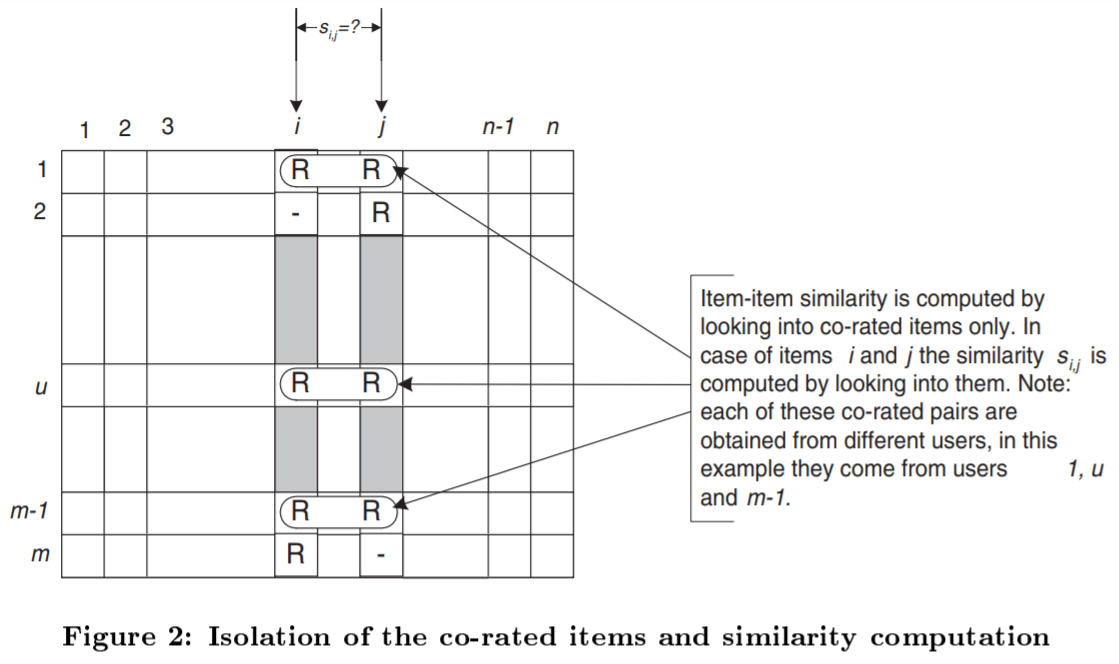
위 그림을 보면 item i,j를 평가한 user의 점수만 유사도 계산에 포함됩니다.
다음으로 점수를 예측하는 방법을 보겠습니다. 저는 regression은 사용하지 않을 거라 Weighted Sum만 보도록 하겠습니다.
2. Predict : Weighted sum
말 그대로 여러 개의 결과를 합쳐 점수를 예측하는 방식입니다. 단, 예측하는 점수는 예측 대상의 user가 평가한 item이면 안됩니다. 식은 다음과 같습니다.
- $P_{u,i} = \frac{ \sum_{all \, similar \, items, \, N} \,(\textbf{s}_{i,N} * R_{u,N} ) }{ \sum_{all \, similar \, items, \, N}\, (| \textbf{s}_{i,N} |) }$
- $P_{u,i}$ : user u의 item i에 대한 예측 점수
- all similar items : item i와 유사도가 있는 모든 데이터를 의미합니다.
- $\textbf{s}_{i,N}$ : item i와 item N의 유사도 값
- $R_{u,N}$ : user u의 item N에 대한 점수
- 분모는 유사도의 절대값의 합입니다.
- 단, 여기서 Correlation과 Adjusted Cosine의 경우 평균값을 빼서 구한 유사도이기 때문에 Predict 값을 구할 때도 마찬가지로 평균값 조정이 필요합니다.
- $P_{u,i} = \bar{R_{u}} + \frac{\sum_{all \, similar \, items, \, N}\, (\textbf{s}_{i,N} *( R_{u,N} - \bar{R_{u}}) ) }{\sum_{all \, similar \, items, \, N}\, (|\textbf{s}_{i,N}|) }$
- 위의 weighted sum과 같은 변수는 똑같은 의미의 변수입니다.
- $\bar{R_{u}}$ : user u의 평균 점수입니다. 이는 item i의 평균 점수로도 바꿀 수 있습니다.
여기까지가 item to item 모델에 대한 설명이었습니다. 저 위의 predict 구하는 부분(weighted sum)이 포인트인데요. 저걸 어떻게 잡느냐에 따라 값이 확 달라지기 때문에 주의가 필요합니다.
이 모델의 특징을 간단히 요약해보면 다음과 같습니다.
○ 특징 : item 간의 유사도를 바탕으로 추천하기 때문에 특정 user에게 item을 추천시 item 구매 이력이 유사한 사람을 활용해 추천함
○ 장점
● 직관적임 : 특정 유저에게 특정 아이템을 추천한 이유가 무엇인지에 대해 분석할 때 item 유사도에 의해 추천한 것이라고 설명 가능
● 복잡한 연산이 없음 : 모델링 할 때 유사도를 사용하고 weighted sum 또는 regression으로 예측하는 단순한 과정입니다.
○ 단점
● Sparsity : 여전히 구매이력이 거의 없는 item은 추천하기 어려운 점이 있습니다.
● Popularity 문제 : 추천이 많이 되는 item은 많이 추천되겠지만 아닌 item은 추천될 가능성이 낮습니다.
● 연산문제 : 복잡한 연산은 없으나 item과 user 숫자가 증가할수록 연산량이 크게 증가하게 됩니다.
다음에는 코드로 구현해보도록 하겠습니다.
감사합니다.
혹시 질문이나 수정할 부분 있으시면 꼭 말씀해주세요!
'모델 > 추천시스템' 카테고리의 다른 글
| Probabilistic Matrix Factorization (알고리즘) (1) | 2020.12.08 |
|---|---|
| Item-Based Collaborative Filtering Recommendation Algorithms (구현) (2) | 2020.12.02 |
| Neural Collaborative Filtering(2) - 알고리즘 및 결과 (0) | 2020.11.15 |
| Neural Collaborative Filtering(1) - 도입부 (0) | 2020.11.10 |
| 추천시스템 - Incremental Singular Value Decomposition Algorithms(2) (0) | 2020.10.14 |


