참고 자료는 다음과 같습니다.
- 파이썬 자료구조와 알고리즘 (한빛미디어, 2019)
- AVL 트리
[자료구조] 균형 잡힌 이진 탐색 트리 : AVL 트리
[자료구조] 균형 잡힌 이진 탐색 트리 : AVL 트리균형 잡힌 이진 탐색 트리, AVL 트리는 이진 탐색...
blog.naver.com
- AVL 트리
lipcoder.tistory.com/entry/AVL-%ED%8A%B8%EB%A6%AC
AVL 트리 (AVL tree)
이진 트리의 문제점 이진 트리의 문제점은 한쪽으로 치우친 형태로 트리 구조가 만들어질 수 있다는 것이다. 이렇게 되면 트리 구조가 아니라 일반적인 연결 리스트와 별 차이가 없는 구조가 되
lipcoder.tistory.com
- AVL의 R, L회전
m.blog.naver.com/beaqon/221298022121
자료구조 AVL트리 회전연산
지난 포스트에서 AVL트리는 네가지 종류의 회전 연산이 있다고 했다. RR, RL, LL, LR이 그 네가...
blog.naver.com
- 균형 트리
빽 투더 기본기 [알고&자구 3편]. 균형 트리
트리의 구조 특성상 탐색의 시간 복잡도가 '대체로' O(log n) 만에 가능하다. 따라서, 파일 시스템 등, 자료를 저장하거나 관리하는 시스템에서 많이 사용되곤 한다. 아무튼 트리를 사용한다는 것
dailyheumsi.tistory.com
이진트리 : 노드가 최대 두 개의 자식 노드를 갖는 자료구조
용어 및 개념
○ 노드 차수 : 자식 수
○ 경로 : 한 노드(부모)에서 다른 노드(자식)로 가는 노드들의 순서
○ 경로 길이 : 한 노드에서 다른 노드로 가는 간선의 수
○ 형제 노드 : 부모가 같은 두 노드
○ 외부 노드(말단 노드) : 자식이 없는 노드(차수가 0)
○ 내부 노드(가지 노드) : 잣ㄱ이 있는 노드(차수가 0이 아닌 노드)
○ 노드 깊이(depth) : 루트 노드에서 어떤 노드로 가는 경로의 길이.
○ 노드 레벨(level) : 루트 노드에서 어떤 노드로 가는 경로의 길이 +1
○ 노드 높이 : 한 노드와 단말 노드 사이의 최대 경로 길이
○ 크기(size) : 모든 노드의 수
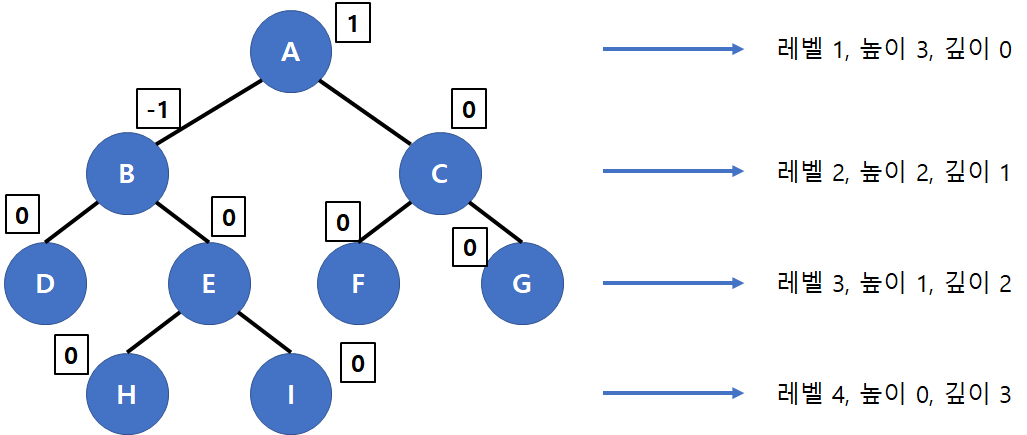
ex)
* 네모의 숫자는 Balance Factor : 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
=> A : 왼쪽 서브트리의 높이가 2, 오른쪽은 1이므로 2-1 = 1
○ 포화 이진 트리
● 모든 내부 노드가 두 개의 자식 노드 가지며 모든 말단 노드가 같은 깊이 또는 레벨을 가짐
○ 완전 이진 트리
● 마지막 레벨을 제외한 모든 레벨이 완전히 채워짐
● 마지막 레벨의 모든 말단 노드는 왼쪽에 우선적으로 있음
○ 이진 트리에서 최대 노드차수는 2임
○ 트리에 m개 내부 노드가 있고, 각 내부 노드에 두 개의 자식 노드가 있다고 가정하며, n개의 말단 노드가 있다면 트리의 차수는 n-1임
● 2m = n+m-1
-> m = n-1
○ 구현 시, 클래스 사용하는 것이 좋음 : 리스트 중간에 노드 삽입하거나 꺼낼 때 제한 있으므로 매우 비효율적
자가 균형 이진 탐색 트리
○ 트리의 사용 목적 : 특정 값에 빠르게 접근하기 위함 * 색인(인덱싱) : 특정 장소(문서)에 데이터를 저장하는 과정 => 편향 트리의 경우 탐색 연산의 시간복잡도가 O(n)으로 되는 문제 발생. 아래 그림을 보면 8을 찾는데 최대 4번의 탐색을 거쳐야 함. * n : 트리의 원소 개수

○ 균형 트리 ● 모든 하위 트리의 높이 차이가 1 이하인 트리 ● 탐색 연산의 시간복잡도를 O(log n)으로 줄일 수 있음
○ 자가 균형 이진 탐색 트리 : 노드의 삽입, 삭제 등의 연산이 발생 시, 자동으로 균형 트리 유지하는 이진 탐색 트리
○ 균형도 : 왼쪽과 오른쪽 하위 트리 높이의 차이
● 노드 분할 및 병합 : 노드 자식은 두 개를 초과 못함
● 노드 회전 : 간선 전환. 예를 들어 a가 b의 부모이면, b를 a의 부모로 하고 a는 b의 자식 중 하나를 가져옴.
○ AVL 트리
● 왼쪽과 오른쪽 하위 트리 높이 차이가 1보다 클 수 없는 자체 균형 조건 가진 이진 탐색 트리
● 균형의 정도를 나타내기 위해 Balance Factor를 사용
* Balance Factor = 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
=> Balance Factor 값이 클수록 불균형도가 큼
● 트리에 노드를 추가 또는 삭제할 때마다 트릐 높이를 계속 확인하며 동작함 : 균형도를 맞추기 위해 오른쪽 또는 왼쪽으로 회전
* Balance Factor가 절대값 1보다 큰 경우 수행
● 회전 예시
□ R회전
■ Balance Factor가 1보다 큰 경우
■ Y의 왼쪽 자식 X를 Y의 자리로 옮기고 Y는 X의 오른쪽 자식이 됨
■ 서브트리 T2를 Y의 왼쪽 자식으로, T3는 Y의 오른쪽 자식으로 옮김

□ R회전

● 삽입 구현
□ 회전 방법 : 균형도가 1보다 큰 경우 LL 케이스의 LR 케이스
■ LL : L회전 1번. 조상 노드의 Y의 왼쪽 서브 트리의 왼쪽 서브 트리에 노드가 추가됐을 때 씀.
■ RR : R회전 1번. 조상 노드의 Y의 오른쪽 서브 트리의 오른쪽 서브 트리에 노드가 추가됐을 때 씀.
■ LR : L회전 1번과 R회전 1번. 조상 노드의 Y의 왼쪽 서브 트리의 오른쪽 서브 트리에 노드가 추가됐을 때 씀.
■ RL : R회전 1번과 L회전 1번. 조상 노드의 Y의 오른쪽 서브 트리의 왼쪽 서브 트리에 노드가 추가됐을 때 씀.
○ 레드-블랙 트리
● 트리 연산 복잡성에 영향 미치지 않으면서 트리 균형 유지하는 것을 목표로 하는 이진 탐색 트리의 개선 버전
● 트리의 노드를 레드, 블랙으로 표시하고 트리 가장 깊은 경로가 가장 짧은 경로의 2배가 되지 않도록 유지하는 방법
● AVL에 비해 덜 균형적이나 노드 삽입, 삭제 과정의 연산이 적음.
○ 이진 힙
● 완전 균형 이진 트리
● 힙 속성 사용
=> 힙의 노드를 분할하거나 회전해 트리 구조 수정할 필요 없음.
'Python > 자료구조' 카테고리의 다른 글
| 그래프 (0) | 2020.10.26 |
|---|---|
| 검색, 동적 계획법 (0) | 2020.10.26 |
| 추상 데이터 타입 (0) | 2020.10.20 |

