참고 자료는 다음과 같습니다.
- 파이썬 자료구조와 알고리즘 (한빛미디어, 2019)
__str__ 과 __repr__
0.__str__과 __repr__ 1. 개요 파이썬에서 매우 자주 쓰이고 은근히 햇갈린느 두 메소드에 대해 다뤄본다. __str_ 과 __repr__로써 이 둘은 객체를 사용자가 이해할 수 있는 문자열로 반환하는 함수다. 2. ��
duwjdtn11.tistory.com
<히프> 기본 개념과 삽입 삭제 알고리즘 정리
# 히프의 개념 히프(heap)는 "더미"라는 뜻이다. 히프는 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조이다. 히프는 간단히 말하면 부모 노드의 키
mattlee.tistory.com
Hash, Hashing, Hash Table(해시, 해싱 해시테이블) 자료구조의 이해
0_HJVxQPQ-eW0Exx7M.jpeg DATA들이 사용하기 쉽게 정리되어 있다. 자료구조는 도대체 무엇일까? 자료구조(Data-Structure)는 데이터들의 모임, 관계, 함수, 명령 등의 집합을 의미한다. 더 쉽게 표현하자면, 1)
velog.io
- dojang.io/mod/page/view.php?id=645
C 언어 코딩 도장: 74.1 연결 리스트 구조체 만들고 사용하기
먼저 연결 리스트의 구조체를 정의합니다. 연결 리스트는 노드들의 집합이므로 실제로는 노드의 구조체만 정의하면 됩니다. ▼ 그림 74‑2 노드 구조체 struct NODE { // 연결 리스트의 노드 구조체 s
dojang.io
추상 데이터 타입
○ 유사한 동작을 가진 자료구조의 클래스에 대한 수학적 모델
○ 자료구조 : 크게 배열 기반의 연속 방식, 포인터 기반의 연결 방식으로 분류됨
● 연속 : 문자열, 리스트, 튜플, 딕셔너리 등
--------------------------------------------------------------------------------------------------
스택
○ 배열 인덱스 접근 제한됨
○ 후입선출(LIFO) 구조 : 나중에 들어온 것이 먼저 나감
=> 마지막에 들어온 것이 제일 먼저 나감
ex) 1,2,3,4,5,6,7,8,9,10을 push 한 다음에 pop하면? -> 10이 나가짐
○ 시간복잡도 : O(1)
○ 깊이 우선 탐색에서 유용하게 사용됨
○ 기능
● push : 스택 맨 끝에 데이터 삽입 (= list의 append())
=> 이전에 온 데이터는 앞으로 옴
● pop : 스택 맨 끝에 있는 데이터 반환 및 제거
● top/peek : 스택 맨 끝 부분 조회
● empty : 스택이 비었는지 확인
● size : 스택 크기 확인
* __repr__ : 사람이 이해할 수 있는 객체 모습으로 반환하도록 하는 메소드
큐
○ 배열 인덱스 접근 제한됨
○ 선입선출(FIFO) 방식 : 먼저 들어온 것이 먼저 나감
ex) 1,2,3,4,5,6,7,8,9,10을 push 한 다음에 pop하면? -> 1이 나가짐
○ 시간복잡도 : O(1)
○ 너비 우선 탐색(BFS)에서 사용됨
○ 기능
● enqueue : 큐 앞쪽에 데이터 삽입
=> 이전에 온 데이터는 뒤로 밀림
● dequeue : 큐 앞쪽의 데이터 반환 및 제거
● peek/front : 큐 앞쪽의 데이터 조회
● empty : 큐 비었는지 확인
● size : 큐 크기 확인
데크
○ 스택과 큐의 결합체
○ 양쪽 끝에서 데이터 조회, 삽입, 삭제 가능
○ from collections import deque로 가능 : 단, 이는 동적 배열이 아닌 이중 연결 리스트를 기반으로 함
힙
○ 각 노드가 하위 노드보다 작은(또는 큰) 이진 트리
○ 균형 트리 모양 수정시, 다시 균형 트리로 만드는 시간복잡도는 O(log n)임
○ 리스트에서 가장 작은(또는 가장 큰) 요소에 반복적으로 접근하는 프로그램에 유용함
○ 최소(최대) 힙 사용시, 가장 작은(큰) 요소 처리하는 시간복잡도는 O(1), 그 외 조회 및 추가, 수정 처리시 시간복잡도는 O(log n)
○ 최대 힙 : 부모의 노드가 자식 노드보다 커야 함.
● 구현 예시 : [3,2,5,1,7,8,2]를 기준으로 했을 때 이를 트리로 나타내고 힙으로 만들어봄
1. 이진 트리로 나타냈을 때 값을 아래와 같이 넣을 수 있음(괄호는 인덱스값)
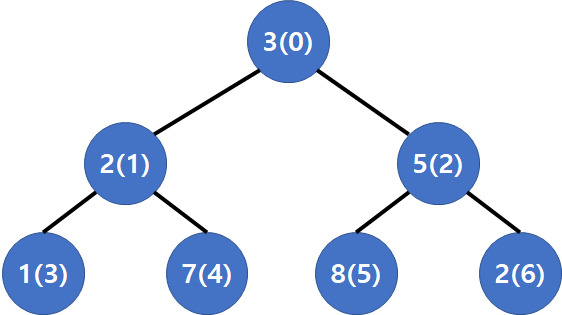
2. 리스트 길이 7을 2로 나눔(나머지 제거) -> 3
3. 3번 (인덱스) 노드의 값부터 2,1,0번 순으로 부모노드가 자식노드보다 작은지 큰지 검사
4. 3번 노드는 자식이 없으므로 통과, 2번 노드는 5이나 5번 노드는 8이므로 2개를 바꿈

5. 교환한 노드 5번부터 아래로 내려가면서 다시 부모 노드와 자식 노드 비교
6. 1번 노드가 자식인 2번 노드보다 작음 : 서로 값 바꿈

7. 2번 노드부터 1,0으로 부모 노드와 자식 노드 비교
8. 0번 노드가 3이나 1번, 2번 자식 노드는 각각 7,8로 0번보다 큼 -> 제일 큰 2번 노드의 8이랑 바꿈

9. 2번 노드가 5번 노드보다 작으므로 두 값을 바꿈

10. 완성
● 구현 예시 : 위의 힙에서 8을 뺀다고 했을 때
1. 가장 마지막 노드(6번)를 8에 해당하는 노드(0번)에 넣음


2. 0번 노드가 1번노드보다 작으므로 두 값을 바꿈

3. 완성
○ 최소 힙 : 부모의 노드가 자식 노드보다 작아야 함.
우선순위 큐
○ 큐랑 구조는 같으나 pop을 하면 들어간 우선순위가 높은 것부터 나옴 : 힙으로 구현
=> 힙으로 하면 root node를 pop하고 다시 순서정리하면 됨
연결 리스트
○ 값과 다음 노드에 대한 포인터(참조)가 포함된 노드로 이루어진 선형 리스트
○ 마지막 노드는 null 값 가짐
○ 연결 리스트로 스택, 큐를 구현 가능
=> 선입선출형, 후입선출형 등 구현
○ 크기가 동적일 수 있어, 저장할 항목 수를 알 수 없을 때 유용함
○ 삽입 시간복잡도 : O(1)
=> 특정 인덱스에 삽입시, O(n)
○ 검색 및 삭제 복잡도 : O(n)
=> 어떤 노드의 포인터를 알고 있을 때 그 노드 삭제하면 삭제 시간복잡도는 O(1)로 됨 : 해당 노드의 값에 다음 노드의 값을 할당하고 해당 노드의 포인터는 다음 다음의 노드를 가리키게 하면 됨
해시 테이블
○ 키를 값에 연결하여 하나의 키가 0 또는 1개의 값과 연관되도록 만듦
○ 키, 해시함수, 해시, 값, 저장소(Bucket, Slot)로 구성됨
○ 키는 해시함수를 통해 해시로 변경되며 해시는 값과 매칭되어 저장소에 저장됨
○ 값 : 저장소에 최종적으로 저장되는 값
○ 해시 충돌 : 두 개의 키가 동일한 버킷에 해시될 때 발생하는 문제
=> 각 버킷에 대해 키-값 쌍의 연결 리스트 저장하여 해결
○ 해시 테이블 조회, 사입, 삭제 시간복잡도 : O(1)
=> 해시 추돌 발생시, 각 작업의 시간복잡도 : O(n)
○ 구조

'Python > 자료구조' 카테고리의 다른 글
| 트리 (0) | 2020.10.27 |
|---|---|
| 그래프 (0) | 2020.10.26 |
| 검색, 동적 계획법 (0) | 2020.10.26 |

